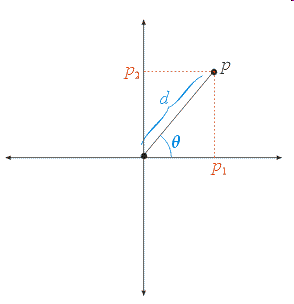Coordinates are quantities that designate the position of a point in relation to a given reference frame. The quantities can be linear and/or angular, and we will consider both here. We will limit our discussion to points on the plane.

In a rectangular coordinate system the reference frame consists of an origin, a basis (more commonly called the coordinate axes), and a directional convention.

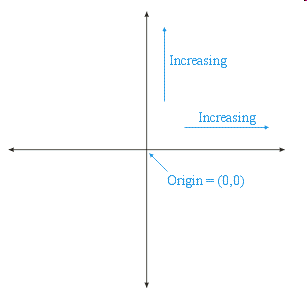
In traditional Cartesian coordinates the origin is at located at the “center” of the plane, the basis consists of the horizontal and vertical axis, and positive values are in the “north east” quadrant (i.e., horizontal coordinates increase from left to right and vertical coordinates increas from down to up). This is illustrated in the following figure.

The horizontal coordinate is traditionally denoted by \(x\) and the vertical coordinate is traditionally denoted by \(y\).

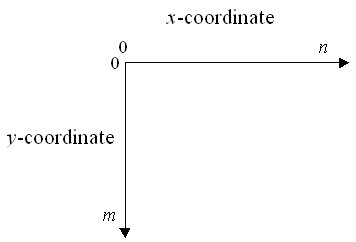
Because of the way old hardware worked, most computer screens/displays do not use Cartesian coordinates. Instead, they use a rectangular system in which the origin is at the upper-left corner, horizontal coordinates increase from left to right, and vertical coordinates increase from up to down (and, as a result, there are no negative coordinates). This is illustrated in the following figure.

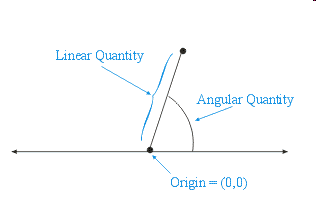
In a polar coordinate system the reference frame consists of and origin located at the “center” of the plane, an angular rotation around origin (in which 0 is to the right the angle increases counter-clockwise), and a linear distance from the origin. Especially in the sciences and engineering, the angular quantity is commonly called the direction and the linear quantity is commonly called the magnitude. This is illustrated in the following figure.

While the angular quantity can be measured in radians or degrees, it is most commonly measured in radians.

One often needs to convert polar coordinates to Cartesian coordinates and vice versa. Fortunately, the process is straightforward and only involves some simple trigonometry.

In the following figure, the point \(p\) can be thought of as either having the Cartesian coordinates \((p_1, p_2)\) or the polar coordinates \((\theta, d)\). When converting from polar coordinates to Cartesian coordinates we have \((\theta, d)\) and must calculate \((p_1, p_2)\). On the other hand, when converting from Cartesian coordinates to polar coordinates we have \((p_1, p_2)\) and must find \((\theta, d)\).

Given \((\theta, d)\) it is clear from the figure that \(\cos(\theta) = p_{1} / d\) and, hence, that \(p_{1} = d \cos(\theta)\). Similarly, it is clear from the figure that \(\sin(\theta) = p_{2} / d\) and, hence, that \(p_{2} = d \sin(\theta)\).

Given \((p_1, p_2)\), on the other hand, it is clear that \(\tan(\theta) = p_2 / p_1\) for \(p_1 \gt 0\) and, hence, that \(\theta = \tan^{-1}(p_{2} / p_{1})\). In addition, observe that \(d\) is the length of the hypotenuse of the right triangle formed by \((p_1, p_2)\). So, it follows that \(d = \sqrt(p_1^2 + p_2^2)\).